Bài tập - Chủ đề 3: Tam giác - Tam giác bằng nhau - Bài tập 3 trang 151 Tài liệu dạy – học Toán 7 tập 1. Giải bài tập Tính số đo x ở các hình 39a, b:
Tính số đo x ở các hình 39a, b:
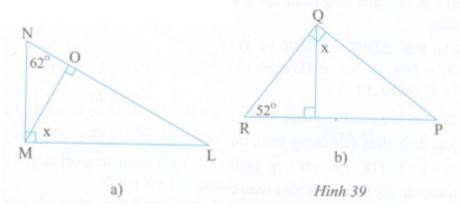
a)Tam giác MON vuông tại O có: \(\widehat {ONM} + \widehat {OMN} = {90^0}\)
Do đó: \({62^0} + \widehat {NMO} = {90^0} \Rightarrow \widehat {NMO} = {90^0} - {62^0} = {28^0}\)
Advertisements (Quảng cáo)
\(\widehat {NMO} + \widehat {LMO} = {90^0}(do\widehat {NML} = {90^0}) \Leftrightarrow {28^0} + x = {90^0} \Rightarrow x = {90^0} - {28^0} = {62^0}\)
b) Tam giác RPQ vuông tại Q có: \(\widehat {QRP} + \widehat {QPR} = {90^0}\)
Do đó: \({52^0} + \widehat {QPR} = {90^0} \Rightarrow \widehat {QPR} = {90^0} - {52^0} = {38^0}\)
\(\widehat P + x = {90^0}\) (hai góc nhọn trong một tam giác vuông)
\( \Rightarrow x = {90^0} - \widehat P = {90^0} - {38^0} = {52^0}\)