
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.
a) Chứng minh rằng tam giác ABM cân.
b) Chứng minh tam giác ABC bằng tam giác MBC.
c) Đường thẳng song song với AB kẻ từ M lần lượt cắt BC, AC tại I và N. Chứng minh đường thẳng AI vuông góc với MC.

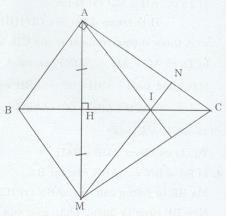
a) Ta có: \(BH \bot AM\) tại H (gt) và H là trung điểm của AM (gt)
=> B thuộc đường trung trực của AM
=> BA = BM
=> ∆ABM cân tại B
b) ∆ABM cân tại B có BH ;à đường cao (\(BH \bot AM\) tại H)
=> BH là đường phân giác của ∆ABM
\( \Rightarrow \widehat {ABC} = \widehat {MBC}\)
Advertisements (Quảng cáo)
Xét ∆ABC và ∆MBC ta có:
AB = BM (câu a)
\(\widehat {ABC} = \widehat {MBC}\)
BC (cạnh chung)
Do đó: ∆ABC = ∆MBC (c.g.c).
a) Ta có: MN // AB (gt)
\(AB \bot AC\) (∆ABC vuông tại A) \( \Rightarrow MN \bot AC\)
∆AMC có: CH là đường cao (\(CH \bot AM\) tại H)
MN là đường cao (\(MN \bot AC\))
CH cắt MN tại I (gt)
Do đó I là trực tâm của ∆AMC => AI là đường cao của ∆AMC
Vậy \(AI \bot MC.\)
