
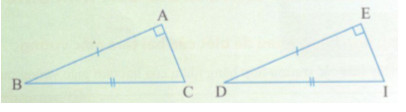
Bài toán : Cho tam giác ABC và tam giác EDI có \(\widehat A = \widehat E = {90^0},BC = DI,AB = ED.\)
Chứng minh rằng \(\Delta ABC = \Delta EDI.\)
Hãy điền vào chỗ trống (….) để hoàn chỉnh phần chứng minh bài toán đã cho :
|
GT |
\(\eqalign{ & \Delta ABC,\widehat A = {90^0} \cr & \Delta EDI,\widehat E = {90^0} \cr & AB = ED,BC = DI \cr} \) |
|
KL |
\(\Delta ABC = \Delta EDI\) |
Chứng minh :
Xét \(\Delta ABC\) vuông tại A, theo định lí Pytagore ta có :
\(B{C^2} = ... + ...\)
Nên \(A{C^2} = ... + ...(1)\)
Xét tam giác EDI vuông tại E, theo định lí Pytagore ta có :
\(... = D{E^2} + E{I^2}\)
Nên \(E{I^2} = ... ...(2)\)
Advertisements (Quảng cáo)
Mà AB = ED, BC = DI (…) (3)
Từ (1), (2), (3) suy ra \(A{C^2} = E{I^2}\) nên AC = …
Từ đó suy ra \(\Delta ABC = \Delta EDI(...)\)

Chứng minh :
Xét \(\Delta ABC\) vuông tại A, theo định lí Pytagore ta có :
\(B{C^2} = A{B^2} + A{C^2}\)
Nên \(A{C^2} = B{C^2} - A{B^2}(1)\)
Xét tam giác EDI vuông tại E, theo định lí Pytagore ta có :
\(D{I^2} = D{E^2} + E{I^2}\)
Nên \(E{I^2} = D{I^2} - D{E^2}(2)\)
Mà AB = ED, BC = DI (gt) (3)
Từ (1), (2), (3) suy ra \(A{C^2} = E{I^2}\) nên AC = EI
Từ đó suy ra \(\Delta ABC = \Delta EDI(c.c.c)\)
