Giải bài tập Em hãy điền các nội dung thích hợp vào chỗ trống để thực hành chứng minh định lí về tính chất ba đường trung trực của tam giác.

Em hãy điền các nội dung thích hợp vào chỗ trống để thực hành chứng minh định lí về tính chất ba đường trung trực của tam giác.
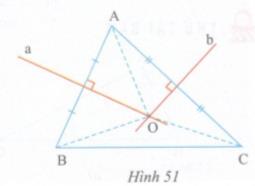
Gọi O là giao điểm của hai đường trung trực ứng với cạnh AB, AC (hình 51). Ta chứng minh O cũng nằm trên đường trung trực ứng với cạnh BC của tam giác ABC và OA = OB = OC.
|
GT |
\(\Delta ABC\) a là đường trung trực AB b là đường trung trực AC a và b cắt nhau tại O |
|
KL |
………………………… ………………………… |
Chứng minh
Ta có : OA = …..(vì O nằm trên đường trung trực a của đoạn thẳng AB)
…..= OC (vì O nằm trên đường trung trực b của đoạn thẳng AC).
Suy ra : …..= …..(= OA).
Do đó điểm …. Nằm trên đường trung trực của cạnh…. Vậy ba đường trung trực của tam guacs ABC cùng đi qua điểm O và ta có :
…. = ….. =….
Chú ý :
Advertisements (Quảng cáo)
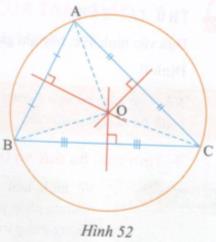
- Vì giao điểm O của ba đường trung trực của tam giác ABC cách đều ba đỉnh của tam giác đó nên có một đường tròn tâm O đi qua ba đỉnh A, B, C.
- Ta gọi đường tròn đó là đường tròn ngoại tiếp tam giác ABC (hình 52).

|
GT |
\(\Delta ABC\) a là đường trung trực AB b là đường trung trực AC a và b cắt nhau tại O |
|
KL |
O nằm trên đường trung trực của BC OA = OB = OC |
Chứng minh
Ta có : OA = OB (vì O nằm trên đường trung trực a của đoạn thẳng AB).
OA = OC (vì O nằm trên đường trung trực b của đoạn thẳng AC).
Suy ra : OB = OC (= OA).
Do đó điểm O nằm trên đường trung trực của cạnh BC.
Vậy ba đường trung trực của tam giác ABC cùng đi qua điểm O và ta có :
OA = OB = OC.
