
Cho tam giác ABC có \(\widehat A = 120^\circ \). Tia phân giác của góc A cắt cạnh BC tại D. Đường thẳng qua D song song với AB cắt cạnh AC tại E. Chứng minh rằng tam giác ADE đều.

Chứng minh tam giác ADE đều ta chứng minh ba góc trong tam giác ADE đều bằng 60°.

Advertisements (Quảng cáo)
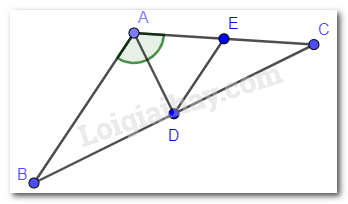
\(\widehat A = 120^\circ \)nên \(\widehat {DAE} = 60^\circ \)(AD là phân giác của góc A).
Ta có: DE // AB nên \(\widehat {CED} = \widehat {EAB} = 120^\circ \)(hai góc đồng vị). Ba điểm A, E, C thẳng hàng nên góc AEC bằng 180°
\(\Rightarrow \widehat {AED} = 180^\circ - \widehat {CED} = 180^\circ - 120^\circ = 60^\circ \)
Tam giác ADE có \(\widehat {EAD} = \widehat {ADE}\) (\(=60^0\)) nên là tam giác cân.
Mà \(\widehat {DEA} = 60^\circ \)
Do đó, tam giác ADE đều ( tam giác cân có 1 góc bằng \(60^0\)).
