
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh tam giác MAB vuông cân.

Ta chứng minh tam giác MAB vuông cân bằng cách chứng minh trong tam giác có một góc vuông tại một đỉnh và có cặp cạnh bằng nhau xuất phát từ đỉnh đó.

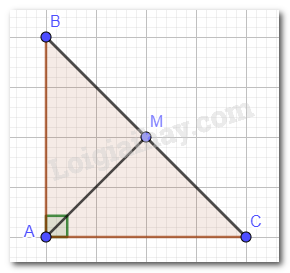
Tam giác ABC vuông cân tại A nên \(\widehat A = 90^\circ ;\widehat B = \widehat C; AB = AC\).
Tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat C = 90:2 = 45^\circ \).
Advertisements (Quảng cáo)
Xét tam giác ABM và tam giác ACM có:
AB = AC
AM chung
BM = CM
\(\Rightarrow \Delta ABM = \Delta ACM\) (c.c.c)
\(\Rightarrow \widehat {BAM} = \widehat {CAM}\) (2 góc tương ứng)
Mà \(\widehat {BAM} + \widehat {CAM}=\widehat{BAC}=90^0\)
\(\Rightarrow \widehat {BAM} = \widehat {CAM} = 90:2 = 45^\circ \).
Xét tam giác MAB: \(\widehat {MBA} = \widehat {BAM} = 45^\circ \Rightarrow \widehat {BMA} = 90^\circ ;MB = MA\).
Vậy tam giác MAB vuông cân tại M.
