III. Dấu hiệu nhận biết
HĐ 3
Cho tam giác ABC thỏa mãn \(\widehat B = \widehat C\). Kẻ AH vuông góc với BC, H thuộc BC (Hình 74).
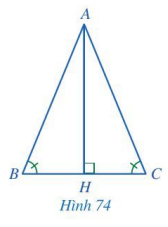
a) Hai tam giác BAH và CAH có bằng nhau hay không? Vì sao?
b) Hai cạnh AB và AC có bằng nhau hay không? Vì sao?

a) Xét hai tam giác BAH và CAH theo trường hợp g.c.g.
b) Sử dụng kết quả phần a) để xét hai cạnh AB và AC. Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau

a) \(\widehat B = \widehat C\). Mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat {BAH} = \widehat {CAH}\).
Xét hai tam giác BAH và CAH có:
\(\widehat {BAH} = \widehat {CAH}\);
Advertisements (Quảng cáo)
AH chung;
\(\widehat {AHB} = \widehat {AHC}\) (= 90°).
Vậy \(\Delta BAH = \Delta CAH\)(g.c.g)
b) \(\Delta BAH = \Delta CAH\) nên AB = AC ( 2 cạnh tương ứng).
LT - VD
Cho tam giác ABC cân tại A. Qua điểm M nằm giữa A và B kẻ đường thẳng song song với BC, cắt cạnh AC tại N. Chứng minh tam giác AMN cân.

Chứng minh tam giác AMN cân bằng cách chứng minh hai góc AMN và ANM bằng nhau.

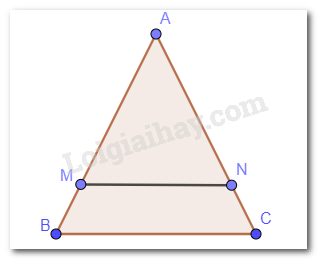
Ta có tam giác ABC cân mà MN // BC. Nên \(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\)(đồng vị)
Mà \(\widehat {ABC} = \widehat {ACB}\)(tam giác ABC cân) nên \(\widehat {AMN} = \widehat {ANM}\).
Vậy tam giác AMN cân tại A ( Tam giác có 2 góc bằng nhau)
