Hướng dẫn giải bài 3 trang 75 SGK Toán lớp 7 tập 1 Chân trời sáng tạo - Bài 2 Tia phân giác
![]()
Cho hai đường thẳng MN, PQ cắt nhau tại A và tạo thành góc PAM = 33º (Hình 9)
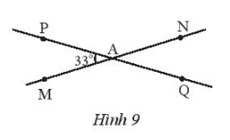
a) Tính số đo các góc còn lại.
b) Vẽ At là tia phân giác của ∠PAN. Hãy tính số đo của ∠tAQ. Vẽ tia At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của ∠MAQ .
![]()
a) Ta có ∠PAM = ∠QAN ( 2 góc đối đỉnh) , mà ∠PAM = 33º nên ∠QAN = 33º
Vì ∠PAN + ∠PAM = 180º ( 2 góc kề bù) nên
∠PAN + 33º = 180º
=> ∠PAN = 180º - 33º = 147º
Vì ∠PAN = ∠QAM ( 2 góc đối đỉnh) , mà ∠PAN = 147º nên ∠QAM = 147º
Advertisements (Quảng cáo)
b) Vẽ tia At là tia phân giác của ∠PAN (như hình vẽ):
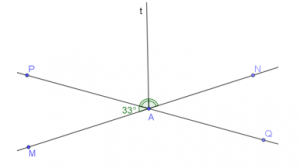
Vì tia At là tia phân giác của ∠PAN nên:
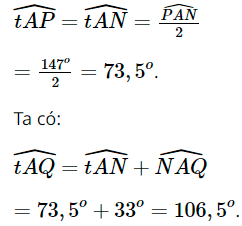
Tia At’ là tia đối của tia At (như hình vẽ).
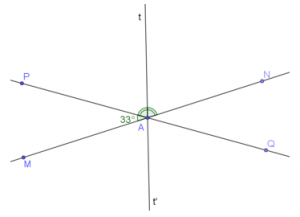
Tia At’ nằm giữa hai tia AM và AQ (1)
Ta có: ∠tAP = ∠t’AQ (hai góc đối đỉnh);
∠tAN = ∠t’AM (hai góc đối đỉnh).
Mà ∠tAP = ∠t’AN (vì tia At là tia phân giác của góc PAN).
Suy ra ∠t’AQ = ∠t’AM (2)
Từ (1) và (2) suy ra: At’ là tia phân giác của góc MAQ
