Vẽ các cung tròn tâm B và tâm C có bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi điểm đó là D. Hãy giải thích vì sao AD vuông góc với đường thẳng a.. Bài 69 trang 141 sgk toán 7 tập 1 - Ôn tập chương II: Tam giác
Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a ở B và C. Vẽ các cung tròn tâm B và tâm C có bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi điểm đó là D. Hãy giải thích vì sao AD vuông góc với đường thẳng a.
Hướng dẫn làm bài:
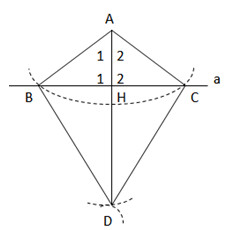
∆ABD và ∆ACD có:
AB = AC (gt)
DB = DC (gt)
AD cạnh chung.
Nên ∆ABD = ∆ACD (c.c.c)
=> \(\widehat {{A_1}} = \widehat {{A_2}}\) (1)
Advertisements (Quảng cáo)
Gọi H là giao điểm của AD và a.
∆AHB và ∆AHC có:
AB = AC (gt)
\(\widehat {{A_1}} = \widehat {{A_2}}\) (1)
AH cạnh chung.
Nên ∆AHB = ∆AHC (c.g.c)
Suy ra: \(\widehat {{H_1}} = \widehat {{H_2}}\)
Ta lại có: \(\widehat {{H_1}} + \widehat {{H_2}} = {180^0} \Rightarrow \widehat {{H_1}} = \widehat {{H_2}} = {90^0}\)
Vậy AD ⊥ a.