Câu hỏi 4 Bài 2 trang 58 SGK Toán 7 Tập 2 : Bài 2. Quan hệ giữa đường vuông góc và đường xiên đường xiên và hình chiếu...

Cho hình $10$. Hãy sử dụng định lí Py-ta-go để suy ra rằng:

a) Nếu $HB > HC$ thì $AB > AC$;

b) Nếu $AB > AC$ thì $HB > HC$;

c) Nếu $HB = HC$ thì $AB = AC$, và ngược lại, nếu $AB = AC$ thì $HB = HC$.

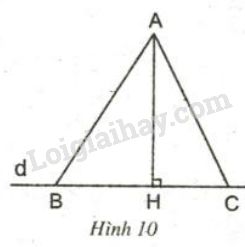
Áp dụng định lí Py-ta-go:

Cho $\Delta ABC$ vuông tại $A$ ta có:

$B{C^2} = A{B^2} + A{C^2}$

Xét tam giác $AHB$ vuông tại $H$

Áp dụng định lí Py-ta-go ta có:

$A{B^2} = A{H^2} + H{B^2}$ (1)

Xét tam giác $AHC$ vuông tại $H$

Áp dụng định lí Py-ta-go ta có:

$A{C^2} = A{H^2} + H{C^2}$ (2)

a) Nếu $HB > HC ⇒ HB^2 > HC^2$.

$⇒ AH^2 + HB^2 > AH^2 + HC^2$

Kết hợp với (1) và (2)

$⇒ AB^2 > AC^2$

$⇒ AB > AC$

b) $AB > AC ⇒ AB^2 > AC^2$

Kết hợp với (1) và (2)

$⇒ AH^2 + HB^2 > AH^2 + HC^2$

$⇒ HB^2 > HC^2$

$⇒ HB > HC$.

c)

- Nếu $HB = HC ⇒ HB^2 = HC^2$.

$⇒ AH^2 + HB^2 = AH^2 + HC^2$

Kết hợp với (1) và (2)

$⇒ AB^2 = AC^2$

$⇒ AB = AC$.

- Nếu $AB = AC ⇒ AB^2 = AC^2$

Kết hợp với (1) và (2)

$⇒ AH^2 + HB^2 = AH^2 + HC^2$

$⇒ HB^2 = HC^2$

$⇒ HB = HC$.