
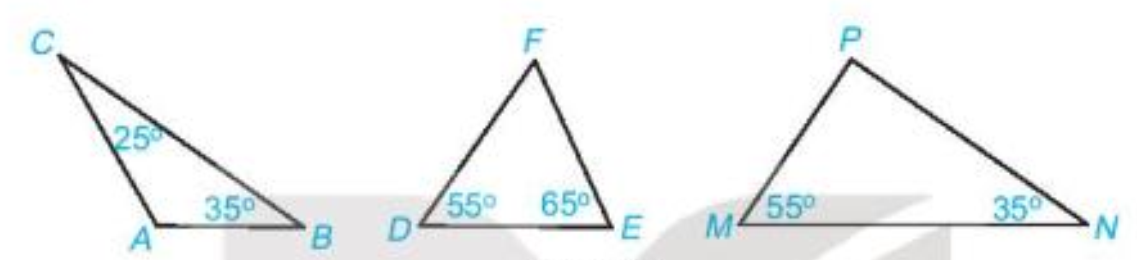
Bài 2 (4.8). Tìm các số đo góc còn lại trong mỗi tam giác dưới đây. Hãy chỉ ra tam giác nào là tam giác vuông.

Tổng ba góc trong một tam giác bằng \({180^o}\).

Vì tổng ba góc trong tam giác ABC bằng \({180^o}\)nên ta có
Advertisements (Quảng cáo)
\(\widehat A + \widehat B + \widehat C = {180^o} \Rightarrow \widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {25^o} - {35^o} = {120^o}\)
Tương tự tròn tam giác DFE ta có
\(\widehat D + \widehat E + \widehat F = {180^o} \Rightarrow \widehat F = {180^o} - \widehat D - \widehat E = {180^o} - {55^o} - {65^o} = {60^o}\)
Cuối cùng trong tam giác MNP ta có
\(\widehat M + \widehat N + \widehat P = {180^o} \Rightarrow \widehat P = {180^o} - \widehat M - \widehat N = {180^o} - {55^o} - {35^o} = {90^o}\)
Kết luận \(\widehat A = {120^o},\widehat F = {60^o},\widehat P = {90^o}\) và chỉ cótam giác MNP có một góc vuông nên chỉ có MNP là tam giác vuông.
