
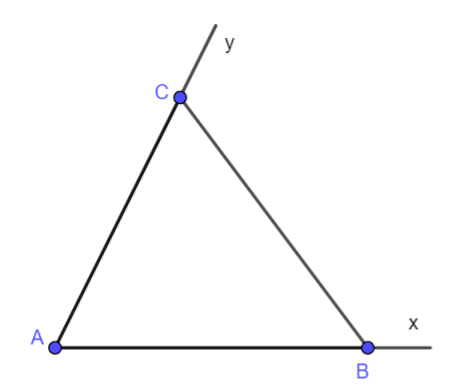
Bài 6. Cho tam giác ABC và cho Bx, Cy lần lượt là các tia đối của các tia BA, CA. Biết \(\widehat {xBC} = \widehat {yCB} = 2\widehat {BAC}\). Hãy tính số đo góc BAC.

Tổng hai góc kề bù và tổng ba góc trong một tam giác bằng \({180^o}\).

|
GT |
\(\Delta ABC\); Bx, Cy là các tia đối của các tia BA,CA; \(\widehat {xBC} = \widehat {yCB} = 2\widehat {BAC}\) |
|
KL |
Advertisements (Quảng cáo) Tính \(\widehat {BAC}.\) |
Vì hai góc kề bù có tổng bằng \({180^o}\)nên ta có:
\(\begin{array}{l}\widehat {ABC} + \widehat {xBC} = {180^o} \Rightarrow \widehat {ABC} = {180^o} - \widehat {xBC}\left( 1 \right)\\\widehat {ACB} + \widehat {yCB} = {180^o} \Rightarrow \widehat {ABC} = {180^o} - \widehat {yCB}\left( 2 \right)\end{array}\)
Do tổng ba góc trong tam giác ABC bằng \({180^o}\)nên ta có:
\(\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\left( 3 \right)\)
Từ (1) , (2) và (3) ta suy ra
\(\begin{array}{l}\widehat {BAC} = {180^o} - \widehat {ABC} - \widehat {ACB}\\ \Leftrightarrow \widehat {BAC} = {180^o} - \left( {{{180}^o} - \widehat {xBC}} \right) - \left( {{{180}^o} - \widehat {yCB}} \right)\\ \Leftrightarrow \widehat {BAC} = 2\widehat {BAC} + 2\widehat {BAC} - {180^o} = 4\widehat {BAC} - {180^o}\end{array}\)
Do đó \(3\widehat {BAC} = {180^o} \Rightarrow \widehat {BAC} = {60^o}\).
