
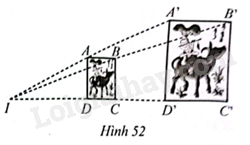
Quan sát Hình 52, biết các điểm .\(A,B,C,D\). lần lượt là trung điểm của các đoạn thẳng \(IA’,IB’,IC’,ID’\).
a) Cho biết hai tứ giác \(ABCD\) và \(A’B’C’D’\) có đồng dạng phối cảnh hay không? Nếu có, hãy chỉ ra tâm đồng dạng phối cảnh.
b) Tứ giác \(A’B’C’D’\) có là hình chữ nhật hay không, nếu tứ giác \(ABCD\) là hình chữ nhật? Vì sao?

Bằng cách “phóng to” (nếu tỉ số vị tự \(k > 1\)) hay “thu nhỏ” (nếu tỉ số vị tự \(k < 1\)) hình \(H\), ta sẽ nhận được hình \(H'\) đồng dạng phối cảnh (hay vị tự) với hình \(H\).
Ta gọi hình \(H’\) là hình đồng dạng phối cảnh (hay vị tự) tỉ số \(k\) của hình \(H\)
Advertisements (Quảng cáo)
Hình đồng dạng phối cảnh tỉ số k của đoạn thẳng \(AB\) là một đoạn thẳng \(A’B’\) (nằm trên đường thẳng song song hoặc trùng với đường thẳng \(AB\)) và \(A’B’ = k.AB\)

a) Tứ giác \(ABCD\) và \(A’B’C’D’\) đồng dạng phối cảnh và \(I\) là tâm đồng dạng phối cảnh.
b) Ta có:
\(\frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}} = \frac{{CD}}{{C’D’}} = \frac{{AD}}{{A’D’}} = \frac{1}{2}\) và \(AB = CD,AD = BC\).
\( = > A’B = C’D’;A’D’ = B’C’\). Do đó, tứ giác \(A’B’C’D’\) là hình bình hành.
Mặt khác, \(AB//A’B’\) và \(BC//B’C’\) nên \(\widehat {A’B’C’} = \widehat {ABC} = 90^\circ \). Do đó, tứ giác \(A’B’C’D’\) là hình chữ nhật.
