
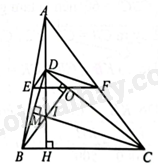
Cho tam giác \(ABC\) có ba góc nhọn, đường cao \(AH\). Trên \(AH,AB,AC\) lần lượt lấy các điểm \(D,E,F\) sao cho \(\widehat {EDC} = \widehat {FDB} = 90^\circ \). Chứng minh: \(EF//BC\).

Định lí Thales đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Advertisements (Quảng cáo)
Kẻ \(BO \bot CD,CM \bot BD,BO\) cắt \(CM\) tại \(I\), suy ra \(D\) là trực tâm của tam giác \(BIC\) hay \(DI \bot BC\).
Mặt khác, \(AH \bot BC = > I,D,A\) thẳng hàng.
Do \(DE//BI\) và \(DF//IC\) nên \(\frac{{AI}}{{AD}} = \frac{{AB}}{{AE}}\) và \(\frac{{AI}}{{AD}} = \frac{{AC}}{{AF}}\)
→ \(\frac{{AB}}{{AE}} = \frac{{AC}}{{AF}}\)
Do đó \(EF//BC\) (định lí Thales đảo).
