
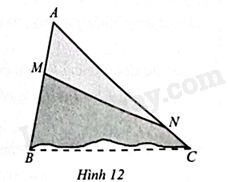
An có một mảnh bìa có dạng hình tam giác \(ABC\) nhưng bị rách. An muốn cắt bỏ phần bị rách với vết cắt là đoạn thẳng \(MN\). Tính diện tích tứ giác \(MNCB\) theo diện tích tam giác \(ABC\), biết \(\frac{{AM}}{{MB}} = \frac{2}{3}\) và \(\frac{{NC}}{{NA}} = \frac{1}{5}\) (Hình 12)

Dựa vào định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Advertisements (Quảng cáo)
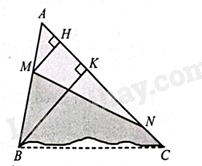
Kẻ đường cao \(MH\) của tam giác \(AMN\) và đường cao \(BK\) của tam giác \(ABC\).
Do \(MH//BK\) nên \(\frac{{MH}}{{BK}} = \frac{{AM}}{{AB}}\)
Ta có \(\frac{{{S_{\Delta AMN}}}}{{{S_{\Delta ABC}}}} = \frac{{\left( {AN.MH} \right):2}}{{\left( {AC.BK} \right):2}} = \frac{{AN}}{{AC}}.\frac{{AM}}{{AB}}\) (1)
Do \(\frac{{AM}}{{MB}} = \frac{2}{3},\frac{{NC}}{{NA}} = \frac{1}{5}\) nên \(\frac{{AM}}{{AB}} = \frac{2}{5},\frac{{AN}}{{AC}} = \frac{5}{6}\) (2)
Từ (1) và (2) suy ra \(\frac{{{S_{\Delta AMN}}}}{{{S_{\Delta ABC}}}} = \frac{{AM}}{{AB}}.\frac{{AN}}{{AC}} = \frac{2}{5}.\frac{5}{6} = \frac{1}{3}\)
→ \({S_{\Delta ABC}} = 3{S_{\Delta AMN}}\)
Từ đó dễ thấy diện tích phần bị cắt bỏ bằng \(\frac{2}{3}{S_{\Delta ABC}}\).
