Bài 2 trang 65 SBT Toán 8 - Chân trời sáng tạo: Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C...

Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD.

a) Chứng minh rằng tứ giác AHCK là hình bình hành.

b) Gọi M là giao điểm của AK và BC, N là giao điểm của CH và AD. Chứng minh $AN = CM.$

c) Gọi O là trung điểm của HK. Chứng minh M, O, N thẳng hàng.

a) Sử dụng kiến thức về dấu hiệu của hình bình hành để chứng minh: Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.

b) Sử dụng kiến thức về dấu hiệu của hình bình hành để chứng minh: Tứ giác có hai cặp cạnh đối song song là hình bình hành.

c) Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.

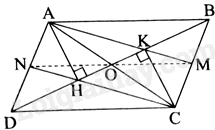
a) Vì ABCD là hình bình hành (gt) nên $AD = BC$, AD//CB. Do đó, $\widehat {HDA} = \widehat {KBC}$ (hai góc so le trong)

Vì $HA \bot BD$ nên $\widehat {AHD} = \widehat {AHB} = {90^0}$

Vì $CK \bot BD$ nên $\widehat {BKC} = \widehat {DKC} = {90^0}$

Tam giác ADH và tam giác CKB có:

$\widehat {AHD} = \widehat {CKB} = {90^0}$, $\widehat {HDA} = \widehat {KBC}$ (cmt), $AD = BC$

Do đó, $\Delta ADH = \Delta CBK\left( {ch - gn} \right)$. Suy ra $AH = KC$.

Tứ giác AHCK có: AH//CK (cùng vuông góc với BD), $AH = KC$ nên tứ giác AHCK là hình bình hành.

b) Vì tứ giác AHCK là hình bình hành nên AK//HC hay AM//NC

Tứ giác ANCM có: AM//NC (cmt), AN//CM (cmt)

Do đó, tứ giác ANCM là hình bình hành.

Suy ra: $AN = CM.$

c) Vì tứ giác AHCK là hình bình hành nên hai đường chéo AC, HK cắt nhau tại trung điểm O của HK nên O là trung điểm của AC.

Vì tứ giác ANCM là hình bình hành nên hai đường chéo AC, NM cắt nhau tại trung điểm O của AC nên O là trung điểm của MN. Do đó, M, O, N thẳng hàng.