
Cho hình bình hành ABCD. Trên các cạnh AB và CD, lần lượt lấy các điểm M và N sao cho \(AM = CN\). Gọi O là giao điểm của MN và AC. Chứng minh rằng ba điểm B, O, D thẳng hàng.

Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
+ Hai cạnh đối song song.

Advertisements (Quảng cáo)
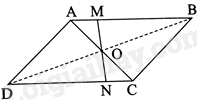
Vì tứ giác ABCD là hình bình hành nên AB//CD. Do đó, \(\widehat {MAO} = \widehat {OCN}\) (hai góc so le trong), \(\widehat {AMO} = \widehat {ONC}\) (hai góc so le trong)
Tam giác MAO và tam giác NCO có:
\(\widehat {MAO} = \widehat {OCN}\) (cmt), \(AM = CN\)(gt), \(\widehat {AMO} = \widehat {ONC}\) (cmt)
Do đó, \(\Delta MAO = \Delta NCO\left( {g - c - g} \right)\)
Suy ra: \(OA = OC\) nên O là trung điểm của AC.
Vì ABCD là hình bình hành nên hai đường chéo AC và BD cắt nhau tại trung điểm O của AC nên O là trung điểm của BD. Suy ra, ba điểm B, O, D thẳng hàng.
