
Cho tam giác ABC vuông tại A, \(AB = 4cm,AC = 8cm.\) Gọi E là trung điểm của AC, M là trung điểm của BC.
a) Tính EM.
b) Vẽ tia Bx song song với AC sao cho Bx cắt EM tại D. Chứng minh tứ giác ABDE là hình vuông.
c) Gọi I là giao điểm của BE và AD, K là giao điểm của BE và AM. Chứng minh tứ giác BDCE là hình bình hành và \(DC = 6KI\).

a) Sử dụng kiến thức: Trong một tam giác, đường thẳng đi qua trung điểm hai cạnh thì song song và bằng \(\frac{1}{2}\) cạnh còn lại.
b) Sử dụng kiến thức về dấu hiệu nhận biết hình vuông để chứng minh: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
c) + Sử dụng kiến thức về tính chất hình vuông để chứng minh: Hình vuông có bốn cạnh bằng nhau.
+ Sử dụng kiến thức về dấu hiệu nhận biết hình bình hành để chứng minh: Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.

Xét bài toán phụ: Cho tam giác ABC có M, N lần lượt là trung điểm của cạnh AB, AC. Lấy P đối xứng với M qua N. Chứng minh rằng MN//BC, \(MN = \frac{{BC}}{2}\)
Chứng minh:
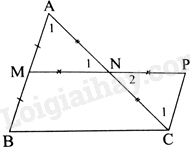
Tam giác AMN và tam giác CPN có:
Advertisements (Quảng cáo)
\(NA = NC\left( {gt} \right),\widehat {{N_1}} = \widehat {{N_2}}\) (hai góc đối đỉnh), \(NM = NP\) (gt)
Do đó, \(\Delta ANM = \Delta CNP\left( {c - g - c} \right)\)
Suy ra \(\widehat {{A_1}} = \widehat {{C_1}}\), mà hai góc này ở vị trí so le trong nên CP//AB hay CP//BM
Lại có: \(CP = AM = BM\)
Tứ giác BMPC có: CP//BM, \(CP = BM\) nên tứ giác BMPC là hình bình hành. Do đó, MN//BC, \(MN = \frac{{BC}}{2}\).
Giải bài 3:
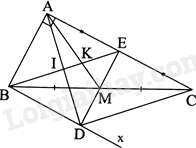
a) Tam giác ABC có E là trung điểm của AC, M là trung điểm của BC nên theo bài toán phụ ta có: \(ME = \frac{1}{2}AB = \frac{1}{2}.4 = 2\left( {cm} \right)\)
b) Tam giác ABC có E là trung điểm của AC, M là trung điểm của BC nên theo bài toán phụ ta có: ME//AB hay DE//AB
Tứ giác ABDE có: DE//AB (cmt), BD//EA (gt) nên tứ giác ABDE là hình bình hành.
Lại có: \(\widehat {BAE} = {90^0}\) nên ABDE là hình chữ nhật.
Vì: \(AE = \frac{1}{2}AC = 4cm = AB\) nên ABDE là hình vuông.
c) Vì E là trung điểm của AC nên \(EC = AE\), mà \(AE = BD\) (do ABDE là hình vuông), suy ra: \(EC = BD\)
Tứ giác BDCE có: \(EC = BD\) (cmt), EC//BD (gt) nên tứ giác BDCE là hình bình hành.
