
Cho hình bình hành ABCD có \(AD = 2AB\). Gọi M là trung điểm của AD. Kẻ CE vuông góc với AB tại E, MF vuông góc với CE tại F, MF cắt BC tại N. Chứng minh rằng:
a) Tứ giác MDCN là hình thoi;
b) Tam giác EMC là tam giác cân;
c) \(\widehat {BAD} = 2\widehat {AEM}\).

a) Sử dụng kiến thức về dấu hiệu nhận biết hình thoi để chứng minh: Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
b) Sử dụng kiến thức về dấu hiệu nhận biết tam giác cân để chứng minh: Tam giác có đường cao đồng thời là đường trung tuyến là tam giác cân.
c) Sử dụng kiến thức về tính chất của hình thoi để chứng minh: Hình thoi có hai đường chéo là các đường phân giác của các góc của hình thoi.

Xét bài toán phụ 1: Cho tam giác ABC có M, N lần lượt là trung điểm của cạnh AB, AC. Lấy P đối xứng với M qua N. Chứng minh rằng MN//BC, \(MN = \frac{{BC}}{2}\).
Chứng minh:
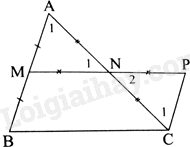
Tam giác AMN và tam giác CPN có:
\(NA = NC\left( {gt} \right),\widehat {{N_1}} = \widehat {{N_2}}\) (hai góc đối đỉnh), \(NM = NP\) (gt)
Do đó, \(\Delta ANM = \Delta CNP\left( {c - g - c} \right)\)
Suy ra \(\widehat {{A_1}} = \widehat {{C_1}}\), mà hai góc này ở vị trí so le trong nên CP//AB hay CP//BM
Lại có: \(CP = AM = BM\)
Tứ giác BMPC có: CP//BM, \(CP = BM\) nên tứ giác BMPC là hình bình hành. Do đó, MN//BC, \(MN = \frac{{BC}}{2}\)
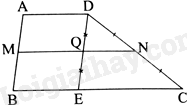
Xét bài toán phụ 2: Cho hình thang ABCD với AD//BC \(\left( {AD < BC} \right)\). Qua điểm D vẽ đường thẳng DE song song với AB (E thuộc BC); gọi N, Q lần lượt là trung điểm của cạnh DC, DE, M là giao điểm của NQ và AB. Chứng minh rằng \(MA = MB\)
Chứng minh:
Advertisements (Quảng cáo)
Xét tam giác DEC có N, Q lần lượt là trung điểm của DC, DE nên NQ//EC, \(NQ = \frac{1}{2}EC\) (theo bài toán phụ 1)
Suy ra: MQ//BE//AD
Theo giả thiết: DE//AB
Tứ giác ADQM có: MQ/ //AD, MA//QD (gt) nên tứ giác ADQM là hình bình hành. Do đó: \(MA = QD\)
Tứ giác MBEQ có: MQ//BE, BM//QE nên tứ giác MBEQ là hình bình hành. Do đó, \(MB = QE\)
Lại có: \(QD = QE\) (gt) suy ra: \(MA = MB\)
Giải bài 5:
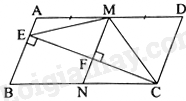
a) Vì ABCD là hình bình hành nên AB//CD, AD//BC
Vì \(MF \bot CE,AB \bot CE\) nên MF//AB. Suy ra: AB//CD//MF
Tứ giác MDCN có: MD//NC (cmt), MN//CD (cmt) nên tứ giác MDCN là hình bình hành.
Lại có: \(MD = \frac{1}{2}AD = CD\) nên MDCN là hình thoi.
b) Xét tứ giác ADCE có: AE//CD (theo câu a)
Do đó, tứ giác ADCE là hình thang.
Hình thang ADCE có: M là trung điểm của AD (giả thiết), AE//MF//CD (theo câu a)
Theo bài toán phụ 2 ta có F là trung điểm của CE.
Xét tam giác ECM có: MF là đường trung tuyến ứng với cạnh CE, \(MF \bot CE\) (gt) nên tam giác EMC cân tại M.
c) Tứ giác MDCN là hình thoi nên \(\widehat {NMD} = 2\widehat {NMC}\) (tính chất đường chéo của hình thoi)
Ta có: \(\widehat {BAD} = \widehat {NMD} = 2\widehat {NMC} = 2\widehat {EMF}\) (1)
Lại có: \(\widehat {AEM} = \widehat {EMF}\) (do AB//MN, hai góc so le trong) (2)
Từ (1) và (2) ta có: \(\widehat {BAD} = 2\widehat {AEM}\)
