Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường. Vận dụng kiến thức giải bài 6 trang 65 sách bài tập (SBT) toán 8 - Chân trời sáng tạo - Bài 4. Hình bình hành - Hình thoi. Cho hình bình hành ABCD. Vẽ hình bình hành AECF \(\left( {E \in AB, F \in CD} \right)\)....

Cho hình bình hành ABCD. Vẽ hình bình hành AECF \(\left( {E \in AB,F \in CD} \right)\). Chứng minh rằng ba đường thẳng EF, AC, BD đồng quy.

Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Advertisements (Quảng cáo)
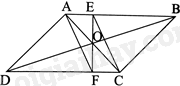
Gọi O là giao điểm của AC và BD.
Vì ABCD là hình bình hành nên O là trung điểm của AC và BD (1)
Vì AECF là hình bình hành nên hai đường chéo AC, EF cắt nhau tại trung điểm O của AC. Do đó, O là trung điểm của EF (2)
Từ (1), (2) ta có: Ba đường thẳng EF, AC, BD đồng quy tại O.
