
Cho hình bình hành ABCD với góc A tù. Dựng bên ngoài hình bình hành đó các tam giác đều ABE và DAF. Chứng minh rằng tam giác CEF là tam giác đều.
(Gợi ý: Chứng minh các tam giác AEF, DCF, BEC bằng nhau)

Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có:
+ Các cạnh đối bằng nhau và song song.
+ Các góc đối bằng nhau.

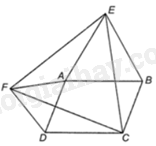
Vì ABCD là hình bình hành nên \(AB = CD,AD = BC\), \(\widehat {ADC} = \widehat {ABC} = {180^0} - \widehat {BAD}\)
Vì \(\Delta \)ABE đều nên \(AE = EB = AB\); \(\widehat {EAB} = \widehat {ABE} = \widehat {AEB} = {60^0}\)
Vì \(\Delta \)ADF đều nên \(AD = DF = AF\); \(\widehat {FAD} = \widehat {FDA} = \widehat {ADF} = {60^0}\)
Advertisements (Quảng cáo)
Ta có: \(\widehat {FAE} = {360^0} - \widehat {EAB} - \widehat {DAB} - \widehat {FAD} = {240^0} - \widehat {DAB}\)
\(\widehat {FDC} = \widehat {FDA} + \widehat {ADC} = {60^0} + {180^0} - \widehat {DAB} = {240^0} - \widehat {DAB}\)
Do đó, \(\widehat {FAE} = \widehat {FDC}\)
Tam giác AEF và tam giác DCF có:
\(AF = DF\left( {cmt} \right),\widehat {FAE} = \widehat {FDC}\left( {cmt} \right),AE = DC\left( { = AB} \right)\)
Suy ra \(\Delta AEF = \Delta DCF\left( {c - g - c} \right)\), do đó, \(FE = CF\left( 1 \right)\)
Ta có: \(\widehat {FDC} = \widehat {FDA} + \widehat {ADC} = {60^0} + \widehat {ABC} = \widehat {ABE} + \widehat {ABC} = \widehat {EBC}\)
Tam giác EBC và tam giác FDC có:
\(BC = DF\left( { = AD} \right),\widehat {EBC} = \widehat {FDC}\left( {cmt} \right),EB = DC\left( { = AB} \right)\)
Suy ra \(\Delta BEC = \Delta DCF\left( {c - g - c} \right)\), do đó, \(EC = CF\left( 2 \right)\)
Từ (1) và (2) ta có: \(EC = CF = FE\) nên tam giác FEC đều.
