
Cho hình vuông ABCD với tâm O và có cạnh bằng 2cm. Hai tia Ox, Oy tạo thành góc vuông. Tính diện tích của phần hình vuông nằm bên trong góc xOy.

Sử dụng tính chất của hình vuông để tính: Hình vuông có hai đường chéo vuông góc với nhau và là các đường phân giác của các góc của hình vuông.

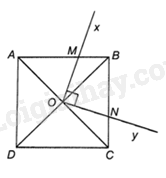
Tia Ox phải cắt một cạnh của hình vuông ABCD. Giả sử Ox cắt cạnh AB tại M.
+ Khi M trùng A hay B thì tia Oy phải đi qua một đỉnh của hình vuông và dễ thấy phần hình vuông nằm trong góc xOy là một phần tư của hình vuông.
+ Khi M nằm giữa A và B thì tia Oy phải cắt cạnh BC hoặc cạnh AD; giả sử tia Oy cắt BC tại N thì N nằm giữa B và C.
Do ABCD là hình vuông nên AC và BD là các đường phân giác của các góc của hình vuông, \(AC \bot BD\) tại O, \(OA = OB\)
Advertisements (Quảng cáo)
Ta có: \(\widehat {MAO} = \widehat {NBO}\left( { = {{90}^0} - \widehat {MBO}} \right)\)
Mà \(\widehat {MOA} + \widehat {MOB} = \widehat {NOB} + \widehat {MOB}\left( { = {{90}^0}} \right)\) nên \(\widehat {MOA} = \widehat {NOB}\)
Tam giác OAM và tam giác OBN có:
\(\widehat {MAO} = \widehat {NBO}\) (cmt), \(OA = OB\)(cmt), \(\widehat {MOA} = \widehat {NOB}\)(cmt)
Do đó, \(\Delta OAM = \Delta OBN\left( {g - c - g} \right)\) nên hai tam giác này có cùng diện tích.
Ta có: Diện tích của phần hình vuông nằm trong góc xOy là diện tích tứ giác OMBN.
Mà \({S_{OMBN}} = {S_{OBM}} + {S_{OBN}};{S_{AOB}} = {S_{OAM}} + {S_{OBM}}\) nên \({S_{OMBN}} = {S_{AOB}}\)
Do đó, diện tích phần hình vuông nằm trong góc xOy bằng \(\frac{1}{4}\) diện tích hình vuông ABCD.
Tương tự khi N nằm giữa A và D thì diện tích của phần hình vuông nằm trong góc xOy bằng \(\frac{1}{4}\) diện tích hình vuông ABCD.
Vậy diện tích cần tìm là: \(\frac{1}{4}{.2^2} = 1\left( {c{m^2}} \right)\)
