Sử dụng kiến thức về đường trung bình của tam giác để chứng minh HI//DK, \(HI = DK\). Giải chi tiết bài 4.8 trang 50 sách bài tập (SBT) toán 8 - Kết nối tri thức với cuộc sống - Bài 16. Đường trung bình của tam giác. Cho tam giác DEF. Gọi H, K, I lần lượt là các trung điểm của DE, DF và EF....

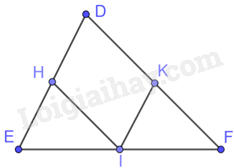
Cho tam giác DEF. Gọi H, K, I lần lượt là các trung điểm của DE, DF và EF. Chứng minh rằng tứ giác HKIE là hình bình hành.

Sử dụng kiến thức về đường trung bình của tam giác để chứng minh HI//DK, \(HI = DK\): Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.

Advertisements (Quảng cáo)
Tam giác DEF có: H, I lần lượt là trung điểm của DE, EF nên HI là đường trung bình của tam giác DEF. Do đó, HI//DF, \(HI = \frac{1}{2}DF\)
Mà K là trung điểm của DF nên \(DK = \frac{1}{2}DF\)
Suy ra: \(HI = DK\)
Tứ giác HDKI có: HI//DK, \(HI = DK\)
Do đó, tứ giác HKIE là hình bình hành.
