
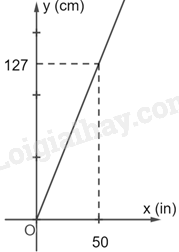
Inch (viết tắt là in) là một đơn vị chiều dài trong hệ đo lường của Mỹ. Phần đường thẳng trong hình vẽ là mô tả sự quy đổi từ x (in) sang y (cm).
a) Tìm hệ số góc của đường thẳng này.
b) Đại lượng y có tỉ lệ thuận với đại lượng x không? Nếu có thì hệ số tỉ lệ bằng bao nhiêu?
c) Đại lượng y có tỉ lệ thuận với đại lượng x không? Nếu có thì hệ số tỉ lệ bằng bao nhiêu?

a) + Vì đường thẳng đi qua gốc tọa độ (và không trùng với hai trục tọa độ) nên nó là đồ thị của hàm số bậc nhất có dạng \(y = ax\left( {a \ne 0} \right)\)
+ Thay tọa độ điểm (50; 127) vào hàm số ta tìm được a.
Advertisements (Quảng cáo)
+ Sử dụng khái niệm hệ số góc của đường thẳng để tìm hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
b) Sử dụng kiến thức về đại lượng tỉ lệ thuận để xác định xem các đại lượng có tỉ lệ thuận với nhau không và tìm hệ số tỉ lệ: Nếu đại lượng y liên hệ với đại lượng x theo công thức \(y = kx\) (với k là hằng số khác) thì ta nói y tỉ lệ thuận với x theo hằng số tỉ lệ k.

a) Vì đường thẳng đi qua gốc tọa độ (và không trùng với hai trục tọa độ) nên nó là đồ thị của hàm số bậc nhất có dạng \(y = ax\left( {a \ne 0} \right)\)
Vì điểm (50; 127) thuộc đồ thị nên \(127 = a.50\), suy ra \(a = \frac{{127}}{{50}} = 2,54\)
Do đó, hệ số góc của đường thẳng là 2,54
b) Vì \(y = 2,54x\) nên đại lượng y tỉ lệ thuận với đại lượng x với hệ số tỉ lệ bằng 2,54
c) Ta có: \(x = \frac{{50}}{{127}}y\) nên đại lượng x cũng tỉ lệ thuận với đại lượng y với hệ số tỉ lệ bằng \(\frac{{50}}{{127}}.\)
