
Cho tam giác ABC và điểm O nằm trong tam giác. Lấy M, N, P là các điểm lần lượt trên các tia OA, OB, OC sao cho \(OA = 3OM,OB = 3ON,OC = 3OP.\) Chứng minh rằng $\Delta ABC\backsim \Delta MNP$ và tìm tỉ số đồng dạng

Sử dụng kiến thức về định lý (trường hợp đồng dạng cạnh – cạnh – cạnh) để chứng minh hai tam giác đồng dạng: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.

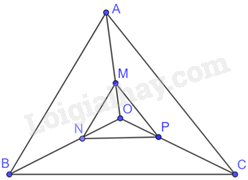
Vì \(OA = 3OM,OB = 3ON,OC = 3OP\) nên \(\frac{{OA}}{{OM}} = 3;\frac{{OB}}{{ON}} = 3;\frac{{OC}}{{OP}} = 3\)
Advertisements (Quảng cáo)
Tam giác OMN có: \(\frac{{OA}}{{OM}} = \frac{{OB}}{{ON}}\) nên AB//MN
Do đó, \(\frac{{AB}}{{MN}} = \frac{{OA}}{{OM}} = 3\)
Chứng minh tương tự ta có: \(\frac{{AC}}{{MP}} = 3;\frac{{BC}}{{NP}} = 3\)
Tam giác ABC và tam giác MNP có:
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}} = 3\)
Do đó, $\Delta ABC\backsim \Delta MNP$ (c.c.c) với tỉ số đồng dạng 3.
