
Cho tam giác ABC có các điểm M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng $\Delta ABC\backsim \Delta MNP$ và tìm tỉ số đồng dạng.

Sử dụng kiến thức về định lý (trường hợp đồng dạng cạnh – cạnh – cạnh) để chứng minh hai tam giác đồng dạng: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.

Advertisements (Quảng cáo)
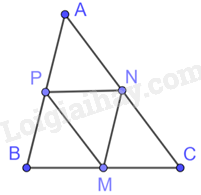
Tam giác ABC có: M, N lần lượt là trung điểm của BC, CA nên MN là đường trung bình của tam giác ABC. Do đó, MN//AB và \(\frac{{AB}}{{MN}} = 2\)
Chứng minh tương tự ta có: \(\frac{{BC}}{{PN}} = 2;\frac{{AC}}{{PM}} = 2\)
Tam giác ABC và tam giác MNP có:
\(\frac{{AB}}{{MN}} = \frac{{BC}}{{PN}} = \frac{{AC}}{{PM}}\left( { = 2} \right)\) nên $\Delta ABC\backsim \Delta MNP$(c.c.c) theo tỉ số đồng dạng là 2.
