
Tính chiều cao và diện tích của một tam giác đều có cạnh bằng 4cm.

+ Sử dụng kiến thức định lí Pythagore để tính độ dài đường cao: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
+ Sử dụng tính chất tam giác đều: Trong tam giác đều, đường cao xuất phát từ đỉnh đồng thời là đường trung tuyến.
+ Sử dụng công thức tính diện tích tam giác để tính diện tích tam giác: Diện tích tam giác bằng nửa tích chiều cao nhân với đáy (chiều cao là chiều cao ứng với đáy đó).

Advertisements (Quảng cáo)
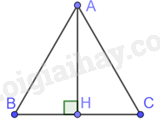
Xét tam giác đều ABC có cạnh \(AB = AC = BC = 4cm\)
Kẻ đường cao AH của tam giác đều ABC.
Khi đó, đường cao AH đồng thời là đường trung tuyến. Do đó, \(AH = \frac{1}{2}BC = \frac{1}{2}.4 = 2\left( {cm} \right)\)
Áp dụng định lý Pythagore vào tam giác ABH vuông tại H có: \(A{H^2} + B{H^2} = A{B^2}\)
\(A{H^2} = A{B^2} - B{H^2} = {4^2} - {2^2} = 12\)
Do đó, \(AH = \sqrt {12} = 2\sqrt 3 \left( {cm} \right)\)
Diện tích tam giác ABC là: \(\frac{1}{2}AH.BC = \frac{1}{2}.4.2\sqrt 3 = 4\sqrt 3 \left( {c{m^2}} \right)\)
