
Hãy liệt kê ba cặp tam giác vuông trong Hình 9.10 đồng dạng và giải thích chúng đồng dạng dựa theo trường hợp nào của hai tam giác vuông đồng dạng?
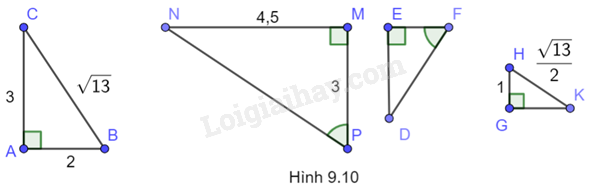

Sử dụng kiến thức các trường hợp đồng dạng của tam giác vuông để tìm các tam giác đồng dạng:
+ Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
+ Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Advertisements (Quảng cáo)
+ Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

Tam giác ABC và tam giác MPN có: \(\widehat A = \widehat M = {90^0},\frac{{AB}}{{MP}} = \frac{{AC}}{{NM}}\left( {do\;\frac{2}{3} = \frac{3}{{4,5}}} \right)\)
Do đó, $\Delta ABC\backsim \Delta MPN\left( cgv-cgv \right)$
Tam giác MNP và tam giác EDF có: \(\widehat M = \widehat E = {90^0},\widehat P = \widehat F\). Do đó, $\Delta MPN\backsim \Delta EFD\left( g-g \right)$
Tam giác ABC và tam giác GHK có: \(\widehat A = \widehat G = {90^0},\frac{{AB}}{{GH}} = \frac{{BC}}{{HK}}\left( {do\;\frac{2}{1} = \frac{{\sqrt {13} }}{{\frac{{\sqrt {13} }}{2}}}} \right)\)
Do đó, $\Delta ABC\backsim \Delta GHK\left( ch-cgv \right)$
