Cho góc xOy, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.
a. Chứng minh rằng OB = OC
b. Tính số đo góc xOy để B đối xứng với C qua O.
Giải:
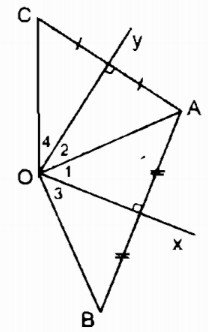
a. Vì B đối xứng với A qua trục Ox nên Ox là đường trung trực của đoạn AB.
⇒ OA = OB (tính chất đường trung trực) (1)
Vì C đối xứng với A qua trục Oy nên Oy là đường trung trực của đoạn AC.
Advertisements (Quảng cáo)
⇒ OA = OC (tính chất đường trung trực) (2)
Từ (1) và (2) suy ra: OB = OC.
b. Ta có: OB = OC do đó điểm B đối xứng với điểm C qua tâm O cần thêm điều kiện B, O, C thẳng hàng.
∆ OAB cân tại O có Ox là đường trung trực của AB nên Ox cũng là đường phân giác của \(\widehat {AOB} \Rightarrow {\widehat O_1} = {\widehat O_3}\)
∆ OAC cân tại O có Oy là đường trung trực của AC nên Oy cũng là đường phân giác của \(\widehat {AOC} \Rightarrow {\widehat O_2} = {\widehat O_4}\)
B, O, C thẳng hàng \( \Leftrightarrow {\widehat O_1} = {\widehat O_2} + {\widehat O_3} + {\widehat O_4} = {180^0}\)
\(\eqalign{& \Leftrightarrow 2{\widehat O_1} + 2{\widehat O_2} = {180^0} \cr& \Leftrightarrow {\widehat O_1} + {\widehat O_2} = {90^0} \cr& \Leftrightarrow \widehat {xOy} = {90^0} \cr} \)
Vậy \(\widehat {xOy} = {90^0}\) thì B đối xứng với C qua tâm O.
