Tam giác cân BAC có BA = BC = a, AC = b. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N
a. Chứng minh rằng: MN // AC.
b. Tính MN theo a, b
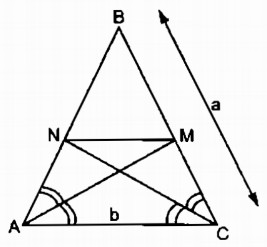

a. Trong tam giác BAC, ta có: AM là đường phân giác của \(\widehat {BAC}\)
Suy ra: \({{MC} \over {MB}} = {{AC} \over {AB}}\) (tính chất đường phân giác ) (1)
CN là đường phân giác \(\widehat {BAC}\)
Suy ra: \({{NA} \over {NB}} = {{AC} \over {AB}}\) (tính chất đường phân giác ) (2)
Lại có: AB = CB = a (gt)
Advertisements (Quảng cáo)
Từ (1), (2) và (gt) suy ra: \({{MC} \over {MB}} = {{NA} \over {NB}}\)
Trong tam giác BAC, ta có: \({{NA} \over {NB}} = {{MC} \over {MB}}\)
Suy ra: MN // AC (theo định lí đảo của định lí Ta-lét)
b. Ta có: \({{MC} \over {MB}} = {{AC} \over {AB}}\) (chứng minh trên )
Suy ra: \({{MC + MB} \over {MB}} = {{AC + AB} \over {AB}} \Rightarrow {{CB} \over {MB}} = {{AC + AB} \over {AB}}\)
Hay \({a \over {MC}} = {{b + a} \over a} \Rightarrow MC = {{{a^2}} \over {a + b}}\)
Trong tam giác ABC, ta có:
MN // AC (chứng minh trên )
Và \({{MN} \over {AC}} = {{MB} \over {BC}}\)
Vậy \(MN = {{AC.MB} \over {BC}} = {{b.{{{a^2}} \over {a + b}}} \over a} = {{ab} \over {a + b}}\)
