Chứng minh rằng đa giác AEHD và hình ABCFE có cùng diện tích.. Câu 23 trang 158 Sách bài tập (SBT) Toán 8 tập 1 - Bài 2. Diện tích hình chữ nhật
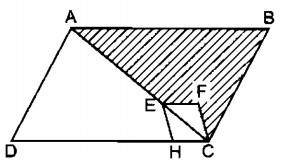
Trên hình 185, các tứ giác ABCD và EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC.
a. Chứng minh rằng đa giác AEHD và hình ABCFE có cùng diện tích.
b. ABCFE có phải là đa giác lồi không ? Vì sao ?
a. Ta có: ∆ ABC = ∆ CDA (c.c.c)
\( \Rightarrow {S_{ABC}} = {S_{CDA}}\) (1)
Advertisements (Quảng cáo)
∆ EFC = ∆ CHE (c.c.c)
\( \Rightarrow {S_{EFC}} = {S_{CHE}}\) (2)
Từ (1) và (2) suy ra:
\({S_{ABC}} - {S_{EFC}} = {S_{CDA}} - {S_{CHE}}\)
Hay \({S_{ABCFE}} = {S_{AEHD}}\)
b. Hình ABCFE không phải tứ giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh CF.