a. Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC.
Chứng minh rằng \({{S’} \over S} = {{DK} \over {AH}}\)
b. Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T.
Chứng minh rằng \({{MH} \over {AD}} + {{MK} \over {BE}} + {{MT} \over {CF}} = 1\)
Giải:
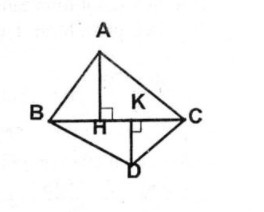
a. Hai ∆ ABC và ∆ DBC có chung canh đáy BC nên ta có:
Advertisements (Quảng cáo)
\(\eqalign{ & {S_{ABC}} = {1 \over 2}AH.BC = S \cr & {S_{DBC}} = {1 \over 2}DK.BC = S’ \cr} \)
Suy ra: \({{S’} \over S} = {{{1 \over 2}DK.BC} \over {{1 \over 2}AH.BC}} = {{DK} \over {AH}}\)
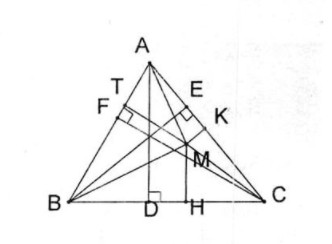
b. Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S1, S2, S3. Ta có:
S = S1 +S2 +S3
Trong đó: S = \({1 \over 2}\)AD. BC = \({1 \over 2}\)BE. AC = \({1 \over 2}\)CF . AB
\(\eqalign{ & {S_1} = {1 \over 2}MT.AB \cr & {S_2} = {1 \over 2}MK.AC \cr & {S_3} = {1 \over 2}MH.BC \cr & {{{S_1}} \over S} = {{{1 \over 2}MT.AB} \over {{1 \over 2}CF.AB}} = {{MT} \over {CF}} \cr & {{{S_2}} \over S} = {{{1 \over 2}MK.AC} \over {{1 \over 2}BE.AC}} = {{MK} \over {BE}} \cr & {{{S_3}} \over S} = {{{1 \over 2}MH.BC} \over {{1 \over 2}AD.BC}} = {{MH} \over {AD}} \cr & \Rightarrow {{MH} \over {AD}} + {{MK} \over {BE}} + {{MT} \over {CF}} = {{{S_3}} \over S} + {{{S_2}} \over S} + {{{S_1}} \over S} = {{{S_1} + {S_2} + {S_3}} \over S} = {S \over S} = 1 \cr} \)
