Tính diện tích toàn phần của hình chóp tam giác đều theo các kích thước cho ở hình 145.. Câu 58 trang 149 Sách bài tập (SBT) Toán 8 tập 2 - Bài 8. Diện tích xung quanh của hình chóp đều
Tính diện tích toàn phần của hình chóp tam giác đều theo các kích thước cho ở hình 145.
(xem hình 145)
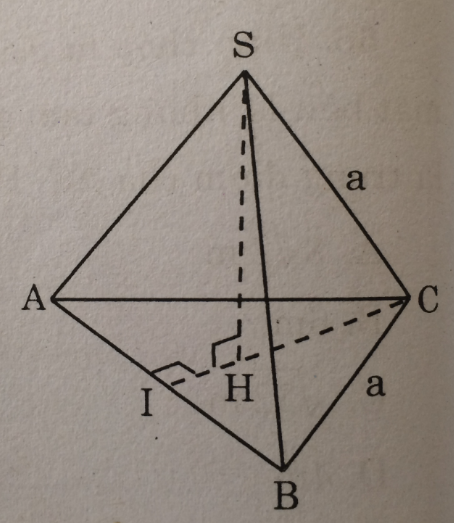

Hình vẽ đã cho là hình chóp có ba mặt xung quanh và mặt đáy là các tam giác đều bằng nhau có cạnh là a. Áp dụng định lí Pi-ta-go vào tam giác vuông CIA, ta có:
Advertisements (Quảng cáo)
Suy ra: \(C{I^2} = A{C^2} - A{I^2} = {a^2} - {\left( {{a \over 2}} \right)^2} = {{3{a^2}} \over 4}\)
Vậy CI = \({{a\sqrt 3 } \over 2}\)
Ta có: \({S_{ABC}} = {1 \over 2}.a.{{a\sqrt 3 } \over 2} = {{{a^2}\sqrt 3 } \over 4}\) (đvdt)
Vậy \({S_{TP}} = 4.{{{a^2}\sqrt 3 } \over 4} = {a^2}\sqrt 3 \) (đvdt)
