Hãy tính thể tích các hình dưới đây (h.143) theo các kích thước cho trên hình vẽ.
(xem hình 143)
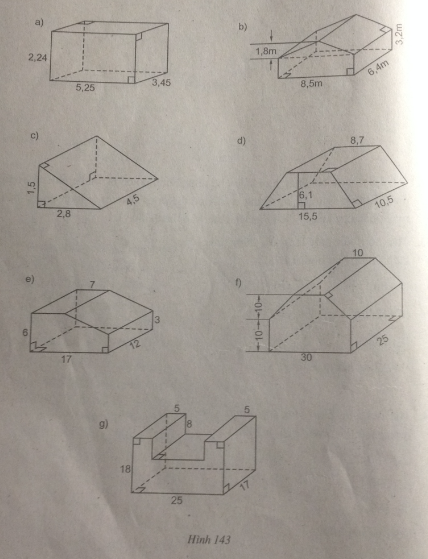

- Hình a:
Ta có: V = S.h = (5,25. 3,45).2,24 = 40,572 (đvtt)
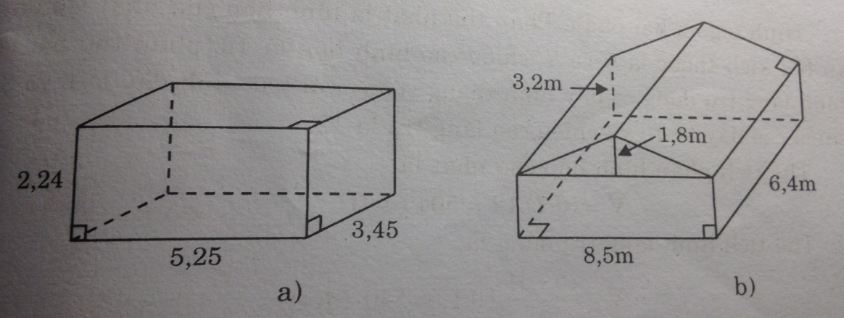
- Hình b:
Hình b gồm một hình hộp chữ nhật và một hình lăng trụ đứng đáy tam giác cân.
Thể tích hình hộp chữ nhật là:
(8,5. 6,4).3,2 = 174,08 (m3)
Thể tích hình lăng trụ là:
\(\left( {{1 \over 2}.8,5.1,8} \right).6,4 = 48,96({m^3})\)
Thể tích hình b là:
V = 174,08 + 48,96 = 223,04 (m3)
- Hình c:
Ta có:
\(V = S.h = \left( {{1 \over 2}.1,5.2,8} \right).4,5 = 9,45\) (đvtt)
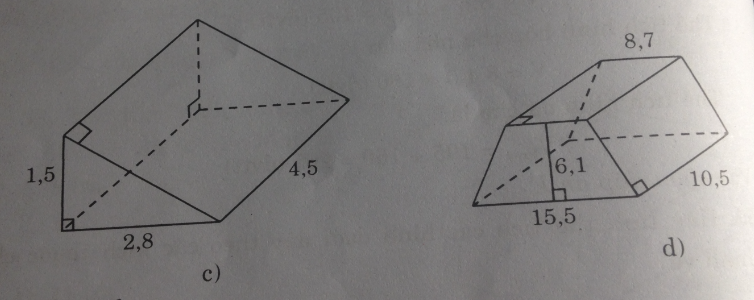
- Hình d:
Ta có:
\(V = {{\left( {8,7 + 15,5} \right)} \over 2}.6,1.10,5 = 775,005\) (đvtt)
- Hình e:
Advertisements (Quảng cáo)
Hình e gồm hai phần. Phần thứ nhất là hình hộp chữ nhật với đáy có hai kích thước là 6 và 7, chiều cao hình hộp là 12; phần thứ hai là hình lăng trụ đứng có đáy hình thang vuông với hai cạnh đáy là 6 và 3, chiều cao đáy là 10 và chiều cao lăng trụ là 12.
Thể tích phần hình hộp chữ nhật là:
V = (6.7).12 = 504 (đvtt)
Thể tích hình lăng trụ đứng là:
V = \({{\left( {6 + 3} \right)} \over 2}.10.12 = 540\) (đvtt)
Thể tích của hình e là:
V = 504 + 540 = 1044 (đvtt)
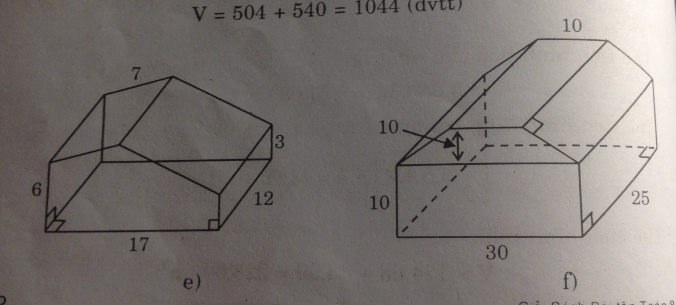
- Hình f:
Hình f gồm hai phần. Phần thứ nhất gồm hình hộp chữ nhật với đáy có hai cạnh là 10 và 30, chiều cao hình hộp 25; phần thứ hai là hình lăng trụ đứng có đáy hình thang với độ dài hai cạnh đáy là 10 và 30, chiều cao đáy là 10 và chiều cao lăng trụ là 25.
Thể tích hình hộp chữ nhật là: \(V = \left( {10.30} \right).25 = 7500\) (đvtt)
Thể tích lăng trụ đứng là: V \( = {{\left( {10 + 30} \right)} \over 2}.10.25 = 5000\) (đvtt)
Thể tích của hình f là: V = 7500 + 5000 = 12500 (đvtt)
- Hình g:
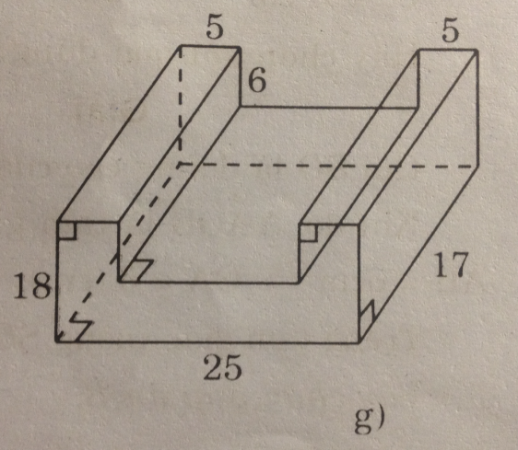
Hình g gồm ba hình hộp chữ nhật. Hai hình hộp chữ nhật có đáy là hình chữ nhật có kích thước là 5 và 8, chiều cao hình hộp 17; một hình hộp chữ nhật có đáy là hình chữ nhật có hai cạnh là 25 và 10 và đường cao hình hộp là 17.
Thể tích hai hình hộp là:
2.(5.8).17 = 1360 (đvtt)
Thể tích hình hộp còn lại là:
(25.10).17 = 4250 (đvtt)
Thể tích hình g là:
V = 1360 + 4250 = 5610 (đvtt)
