. Câu 61 trang 150 Sách bài tập (SBT) Toán 8 tập 2 - Bài 8. Diện tích xung quanh của hình chóp đều
Hình chóp đều S.ABC có cạnh đáy a = 12cm, chiều cao h = 8cm. Hãy tính diện tích xung quanh của hình chóp đó.
Giải:
(hình trang 155 sgbt)
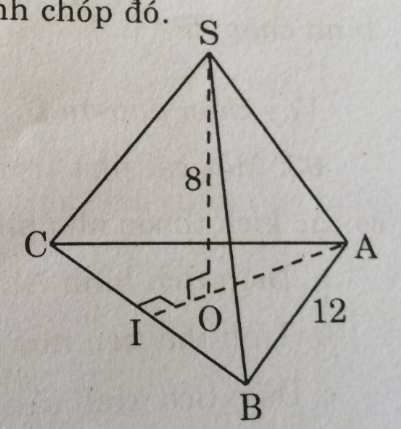
Kẻ AO kéo dài cắt BC tại I.
Ta có: AI ⊥ BC (tính chất tam giác đều)
BI = IC = \({1 \over 2}BC\)
Áp dụng định lí Pi-ta-go vào tam giác vuông AIB, ta có: $A{B^2} = B{I^2} + A{I^2}$
Advertisements (Quảng cáo)
Suy ra:
\(\eqalign{ & A{I^2} = A{B^2} - B{I^2} = {12^2} - {6^2} = 108 \cr & AI = \sqrt {108} (cm) \cr} \)
Vì tam giác ABC đều nên O là trọng tâm của tam giác ABC.
Ta có: \(OI = {1 \over 3}AI = {1 \over 3}\sqrt {108} \) (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông SOI, ta có:
\(\eqalign{ & S{I^2} = S{O^2} + O{I^2} = {8^2} + {1 \over 9}.108 = 76 \cr & SI = \sqrt {76} (cm) \cr} \)
Vậy \({S_{xq}} = Pd = \left[ {\left( {12.3} \right):2} \right].\sqrt {76} = 18\sqrt {76} (c{m^2})\)
