Chứng minh rằng AC + CB < AM + MB.. Câu 67 trang 87 Sách bài tập (SBT) Toán 8 tập 1 - Bài 6. Đối xứng trục
Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C (M khác C). Chứng minh rằng AC + CB < AM + MB.
Giải:
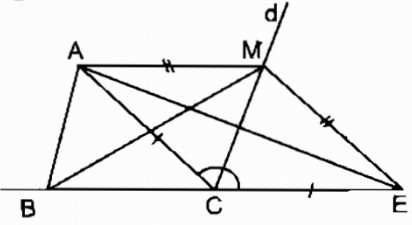
Trên tia đối tia CB lấy điểm E sao cho CE = CA. Nối MA, ME nên ∆ ACE cân tại C có CM là đường trung trực (tính chất tam giác cân)
⇒ MA = ME ( tính chất đường trung trực)
Advertisements (Quảng cáo)
Ta có: AB + BC = BC + CE = BE (1)
MA + MB = MB + ME (2)
Trong ∆ MBE ta có: BE < MB + ME ( bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AB + BC = MA + MB
