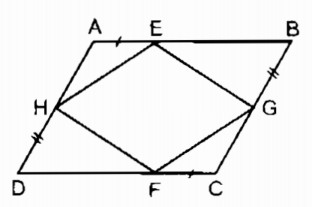
Trên hình 11, cho ABCD là hình bình hành. Chứng minh rằng:
a. EGFH là hình bình hành
b. Các đường thẳng AC, BD, EF, GH đồng quy.
Giải:
a. Xét ∆ AEH và ∆ CFG:
AE = CF
\(\widehat A = \widehat C\) (tính chất hình bình hành)
AH = CG (vì AD = BC và DH = BG)
Do đó: ∆ AEH = ∆ CFG (c.g.c)
⇒ EH = FG
Xét ∆ BEG và ∆DFH:
DH = BG (gt)
Advertisements (Quảng cáo)
\(\widehat B = \widehat D\) (tính chất hình bình hành)
BE = DF (vì AB = CD và AE = CF)
Do đó: ∆ BEG = ∆DFH (c.g.c)
⇒ EG = FH
Suy ra: Tứ giác EGFH là hình bình hành (vì có cắc cặp cạnh đối bằng nhau)
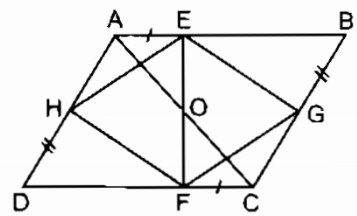
b. Gọi O là giao điểm của AC và EF.
Xét tứ giác AECF:
AB // CD (gt) hay AE // CF
AE = CF (gt)
Suy ra: Tứ giác AECF là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau)
⇒ O là trung điểm của AC và EF
Tứ giác ABCD là hình bình hành có O là trung điểm của AC nên O cũng là trung điểm của BD.
Tứ giác EGFH là hình bình hành có O là trung điểm của EF nên O cùng là trung điểm của GH.
Vậy AC, BD, GH đồng quy tại O.
