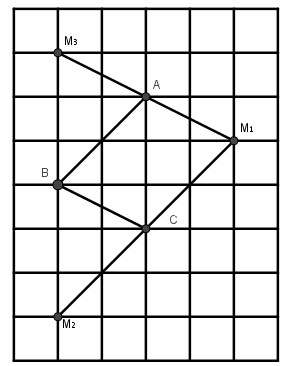
Cho ba điểm A, B, C trên giấy kẻ ô vuông (h.12). Hãy vẽ điểm thứ tư M sao cho A, B, C, M là bốn đỉnh của một hình bình hành

Giải:
Advertisements (Quảng cáo)
- Nếu hình bình hành nhận AC làm đường chéo vì AB là đường chéo hình vuông có cạnh là hai ô vuông nên \(C{M_1}\) là đường chéo hình vuông cạnh 2 ô vuông và A, \({M_1}\)nằm trên nửa mặt phẳng bờ BC ta có hình bình hành \(ABC{M_1}\) .
- Nếu hình bình hành nhận BC làm đường chéo, điểm A cách điểm C ba ô vuông , điểm B cách \({M_2}\) là ba ô vuông và C, \({M_2}\)cũng nằm trên nửa mặt phẳng bờ AB ta có hình bình hành \(AB{M_2}C\)
- Nếu hình bình hành nhận AB làm đường chéo thì điểm \({M_3}\) cách điểm B ba ô vuông, \({M_3}\)và A nằm trên cũng một nửa mặt phẳng bờ BC ta có hình bình hành \(ACB{M_3}\) .
