
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB. Chứng minh tứ giác MNPQ là hình vuông.

Chứng minh tứ giác MNPQ là hình thoi có một góc vuông nên MNPQ là hình vuông

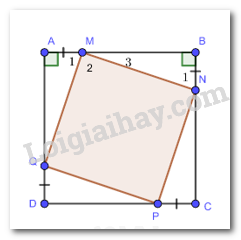
Ta có: AM = BN = CP = DQ (gt)
AB = BC = CD = DA (ABCD là hình vuông)
Advertisements (Quảng cáo)
\(\Rightarrow\) BM = CN = DP = AQ
\(\Rightarrow \Delta AMQ = \Delta BNM = \Delta CPN = \Delta DQP\)(hai cạnh góc vuông)
Suy ra QM = MN = NP = PQ
Suy ra MNPQ là hình thoi
Do: \(\Delta AMQ = \Delta BNM \Rightarrow {\widehat M_1} = \widehat {BNM}\) (2 góc tương ứng)
Mà: \(\widehat {BNM} + {\widehat M_3} = {90^0}\)(do \(\Delta BNM\)vuông tại B)
\( \Rightarrow {\widehat M_1} + {\widehat M_3} = {90^0} \Rightarrow {\widehat M_2} = {180^0} - {\widehat M_1} - {\widehat M_3} = {180^0} - {90^0} = {90^0}\)
Vậy hình thoi MNPQ có một góc bằng 90o nên MNPQ là hình vuông
