Chứng minh tứ giác CDEG là hình bình hành có một góc vuông nên CDEG là hình chữ nhật. Giải chi tiết bài 9 trang 121 SGK Toán 8 tập 1 - Cánh diều Bài tập cuối chương 5. Cho tam giác ABC vuông cân tại C...
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm D, G sao AD = CG < AC. Từ điểm D kẻ DE vuông góc với AC (E thuộc AB). Chứng minh tứ giác CDEG là hình chữ nhật.
Chứng minh tứ giác CDEG là hình bình hành có một góc vuông nên CDEG là hình chữ nhật.
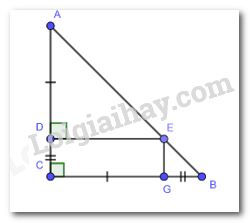
Vì \(\Delta ABC\) vuông cân tại C.
\( \Rightarrow \widehat {C{\rm{AB}}} = {45^0} \Rightarrow \widehat {DA{\rm{E}}} = {45^0}\)
Advertisements (Quảng cáo)
\(\Rightarrow \widehat {DE{\rm{A}}} = {45^0} \Rightarrow \Delta ADE\) là tam giác vuông cân tại D
Suy ra AD = DE (1)
Mà: AD = CG (2)
Từ (1), (2) suy ra: DE = CG.
Mặt khác DE//CG (vì cùng vuông góc với AC)
Suy ra tứ giác CDEG là hình bình hành
Mặt khác: \(\widehat {DCG} = {90^0}\)
Suy ra hình bình hành CDEG là hình chữ nhật