
Cho tam giác \(ABC\) nhọn có hai đường cao \(BM,CN\) cắt nhau tại \(H\).
a) Chứng minh rằng \(\Delta AMN\backsim\Delta ABC\).
b) Phân giác của \(\widehat {BAC}\) cắt \(MN\) và \(BC\) lần lượt tại \(I\) và \(K\). Chứng minh rằng \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\).

- Trường hợp đồng dạng thứ ba của tam giác góc – góc.
- Trường hợp đồng dạng thứ hai của tam giác cạnh – góc – cạnh.
- Hai tam giác đồng dạng thì chúng có các cặp cạnh tương ứng có cùng tỉ lệ.
- Tính chất đường phân giác.

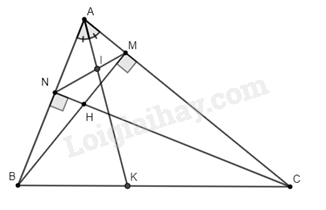
a) Vì \(BM\) là đường cao nên \(\widehat {AMB} = 90^\circ \); vì \(CN\) là đường cao nên \(\widehat {ANC} = 90^\circ \)
Xét tam giác \(AMB\) và tam giác \(ANC\) có:
\(\widehat A\) (chung)
\(\widehat {ANB} = \widehat {ANC} = 90^\circ \) (chứng minh trên)
Advertisements (Quảng cáo)
Suy ra, \(\Delta AMB\backsim\Delta ANC\) (g.g).
Suy ra, \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (tỉ lệ thức)
Xét tam giác \(AMN\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (chứng minh trên)
Suy ra, \(\Delta AMN\backsim\Delta ABC\) (c.g.c).
b) Xét tam giác \(AMN\) có \(AI\) là đường phân giác của \(\widehat {MAN}\left( {I \in MN} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{IM}}{{IN}} = \frac{{AM}}{{AN}}\)
Xét tam giác \(ABC\) có \(AK\) là đường phân giác của \(\widehat {BAC}\left( {K \in BC} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{BK}}{{KC}} = \frac{{AB}}{{AC}}\)
Mà \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (chứng minh trên) nên \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\) (điều phải chứng minh).
