
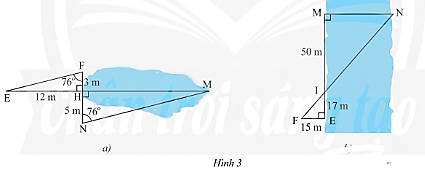
a) Tính khoảng cách \(HM\) của mặt hồ ở Hình 3a.
b) Tính khoảng cách \(MN\) của một khúc sông ở Hình 3b.

- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
- Nếu \(\Delta ABC\backsim\Delta A’B’C’\) thì \(\frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}} = \frac{{BC}}{{B’C’}} = k\)

a) Xét tam giác \(EFH\) và tam giác \(MNH\) có:
\(\widehat {EFH} = \widehat {MNH} = 76^\circ \) (giả thuyết)
\(\widehat {EHF} = \widehat {NHM} = 90^\circ \) (giải thuyết)
Advertisements (Quảng cáo)
Suy ra, \(\Delta EFH\backsim\Delta MNH\) (g.g)
Suy ra, \(\frac{{EH}}{{MH}} = \frac{{FH}}{{NH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{12}}{{MH}} = \frac{3}{5} \Rightarrow MH = 12.5:3 = 20\).
Vậy khoảng cách \(HM\) của mặt hồ là 20m.
b) Xét tam giác \(MNI\) và tam giác \(EFI\) có:
\(\widehat {MIN} = \widehat {EIF}\) (hai góc đối đỉnh)
\(\widehat {NMI} = \widehat {FEI} = 90^\circ \) (giải thuyết)
Suy ra, \(\Delta MNI\backsim\Delta EFI\) (g.g)
Suy ra, \(\frac{{MI}}{{EI}} = \frac{{MN}}{{EF}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{50}}{{17}} = \frac{{MN}}{{15}} \Rightarrow MN = 50.15:17 = \frac{{750}}{{17}}\).
Vậy khoảng cách \(MN\) của mặt hồ là sấp sỉ 44m.
