
Cho tam giác \(ABC\) vuông tại \(A\left( {AB < AC} \right)\). Kẻ đường cao \(AH\left( {H \in BC} \right)\).
a) Chứng minh rằng \(\Delta ABH\backsim\Delta CBA\), suy ra \(A{B^2} = BH.BC\).
b) Vẽ \(HE\) vuông góc với \(AB\) tại \(E\), vẽ \(HF\) vuông góc với \(AC\) tại \(F\). Chứng minh rằng \(AE.AB = AF.AC\).
c) Chứng minh rằng \(\Delta AFE\backsim\Delta ABC\).
d) Qua \(A\) vẽ đường thẳng song song với \(BC\) cắt đường thẳng \(HF\) tại \(I\). Vẽ \(IN\) vuông góc với \(BC\) tại \(N\). Chứng minh rằng \(\Delta HNF\backsim\Delta HIC\).

- Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
- Nếu tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
- Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đồng dạng với nhau.

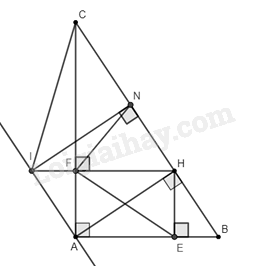
a) Vì \(AH\) là đường cao nên \(\widehat {AHB} = \widehat {AHC} = 90^\circ \)
Xét tam giác \(ABH\) và tam giác \(CBA\) có:
\(\widehat B\) (chung)
\(\widehat {AHB} = \widehat {CAB} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta ABH\backsim\Delta CBA\) (g.g).
Do đó, \(\frac{{AB}}{{CB}} = \frac{{BH}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(A{B^2} = BH.BC\) .
b)
- Vì \(HE\) vuông góc với \(AB\) nên \(\widehat {HEA} = \widehat {HEB} = 90^\circ \)
Xét tam giác \(AHE\) và tam giác \(ABH\) có:
\(\widehat {HAE}\) (chung)
\(\widehat {HEA} = \widehat {AHB} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AHE\backsim\Delta ABH\) (g.g).
Do đó, \(\frac{{AH}}{{AB}} = \frac{{AE}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Advertisements (Quảng cáo)
Suy ra, \(A{H^2} = AB.AE\) . (1)
- Vì \(HF\) vuông góc với \(AC\) nên \(\widehat {HFC} = \widehat {HFA} = 90^\circ \)
Xét tam giác \(AHF\) và tam giác \(ACH\) có:
\(\widehat {HAF}\) (chung)
\(\widehat {AFH} = \widehat {AHC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AHF\backsim\Delta ACH\) (g.g).
Do đó, \(\frac{{AH}}{{AC}} = \frac{{AF}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(A{H^2} = AF.AC\) . (2)
Từ (1) và (2) suy ra, \(AE.AB = AF.AC\) (điều phải chứng minh)
c) Vì \(AE.AB = AF.AC \Rightarrow \frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\).
Xét tam giác \(AFE\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\) (chứng minh trên)
Suy ra, \(\Delta AFE\backsim\Delta ABC\) (c.g.c).
d) Vì \(HF\) vuông góc với \(AC\) nên \(CF \bot HI\), do đó, \(\widehat {CFH} = \widehat {CFI} = 90^\circ \).
Vì \(IN \bot CH \Rightarrow \widehat {CBI} = \widehat {HNI} = 90^\circ \).
Xét tam giác \(HFC\) và tam giác \(HNI\) có:
\(\widehat {CHI}\) (chung)
\(\widehat {HFC} = \widehat {HNI} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta HFC\backsim\Delta HNI\) (g.g).
Suy ra, \(\frac{{HF}}{{HN}} = \frac{{HC}}{{HI}}\) (hai cặp cạnh tương ứng cùng tỉ lệ)
Do đó, \(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\).
Xét tam giác \(HNF\) và tam giác \(HIC\) có:
\(\widehat {CHI}\) (chung)
\(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\) (chứng minh trên)
Suy ra, \(\Delta HNF\backsim\Delta HIC\) (c.g.c).
