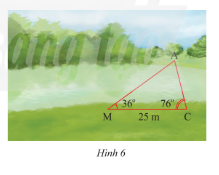
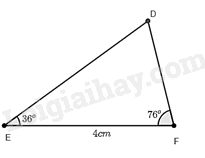
Quan sát Hình 6. Vẽ vào tờ giấy tam giác \(DEF\) với \(EF = 4cm,\widehat E = 36^\circ ,\widehat F = 76^\circ \).
a) Chứng minh \(\Delta DEF\backsim\Delta AMC\).
b) Dùng thước đo chiều dài cạnh \(DF\) của \(\Delta DEF\). Tính khoảng cách giữa hia điểm \(A\) và \(C\) ở hai bờ sông trong Hình 6.
- Nếu hai góc của một tam giác này bằng hai góc tương ứng của một tam giác kia thì hai tam giác đó đồng dạng.
a) Xét tam giác \(DEF\) và tam giác \(AMC\) có:
\(\widehat E = \widehat M = 36^\circ \)
\(\widehat F = \widehat C = 76^\circ \) (chứng minh trên)
Suy ra, \(\Delta DEF\backsim\Delta AMC\) (g.g).
b) Đổi 25m = 2500 cm.
Dùng thước đo độ dài cạnh \(DF\) ta được độ dài \(DF\) là 2,6cm.
Vì \(\Delta DEF\backsim\Delta AMC\) nên \(\frac{{DF}}{{EF}} = \frac{{AC}}{{MC}}\) (hai cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{2,6}}{4} = \frac{{AC}}{{2500}} \Rightarrow AC = \frac{{2,6.2500}}{4} = 1625\).
Vậy khoảng cách giữa hai điểm \(A\) và \(C\) là 1625 cm hay 16,25m.