
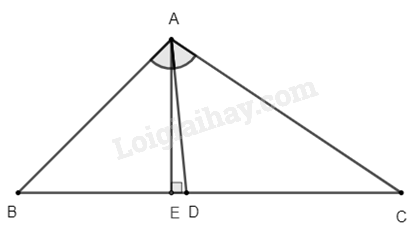
Tam giác \(ABC\) có \(AB = 6cm,AC = 8cm,BC = 10cm\). Đường phân giác của góc \(BAC\) cắt cạnh \(BC\) tại \(D\).
a) Tính độ dài các đoạn thẳng \(DB\) và \(DC\).
b) Tính tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\).

- Sử dụng Tính chất đường phân giác trong tam giác:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.
- Diện tích tam giác
\(S = \frac{1}{2}a.h\) với \(a\) là độ dài đáy và \(h\) là chiều cao.

a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 10 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
Advertisements (Quảng cáo)
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{10 - BD}} = \frac{6}{8} \Leftrightarrow 8BD = 6.\left( {10 - BD} \right) \Rightarrow 8BD = 60 - 6BD\)
\( \Leftrightarrow 8BD + 6BD = 60 \Leftrightarrow 14BD = 60 \Rightarrow BD = \frac{{60}}{{14}} = \frac{{30}}{7}\)
\( \Rightarrow DC = 10 - \frac{{30}}{7} = \frac{{40}}{7}\)
Vậy \(BD = \frac{{30}}{7}cm;DC = \frac{{40}}{7}cm\).
b) Kẻ \(AE \bot BC \Rightarrow AE\) là đường cao của tam giác \(ABC\).
Vì \(AE \bot BC \Rightarrow AE \bot BD \Rightarrow AE\)là đường cao của tam giác \(ADB\)
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = \frac{1}{2}BD.AE\)
Vì \(AE \bot BC \Rightarrow AE \bot DC \Rightarrow AE\)là đường cao của tam giác \(ADC\)
Diện tích tam giác \(ADC\) là:
\({S_{ADC}} = \frac{1}{2}DC.AE\)
Ta có: \(\frac{{{S_{ADB}}}}{{{S_{ADC}}}} = \frac{{\frac{1}{2}AE.BD}}{{\frac{1}{2}AE.CD}} = \frac{{BD}}{{DC}} = \frac{{\frac{{30}}{7}}}{{\frac{{40}}{7}}} = \frac{3}{4}\).
Vậy tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\) là \(\frac{3}{4}\).
