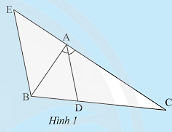
Cho tam giác \(ABC\) có đường phân giác \(AD\). Vẽ đường thẳng qua \(B\) song song với \(AD\) và cắt đường thẳng \(AC\) tại \(E\) (Hình 1). Hãy giải thích tại sao:
a) Tam giác \(BAE\) cân tại \(A\).
b) \(\frac{{DB}}{{DC}} = \frac{{AE}}{{AC}} = \frac{{AB}}{{AC}}\).
- Nếu một đường thẳng cắt hai đường thẳng song song sẽ tạo ra các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.
- Định lí Thales.
a) Vì \(BE//AD\) nên \(\widehat {EBA} = \widehat {BAD}\) (cặp góc so le trong) (1)
Vì \(BE//AD\) nên \(\widehat {BEA} = \widehat {DAC}\) (cặp góc đồng vị) (2)
Vì \(AD\) là tia phân giác nên \(\widehat {BAD} = \widehat {DAC}\) (tính chất) (3)
Từ (1); (2); (3) suy ra \(\widehat {EBA} = \widehat {AEB}\)
Xét tam giác \(BAE\) có:
\(\widehat {EBA} = \widehat {AEB}\) (chứng minh trên)
Nên tam giác \(BAE\) cân tại \(A\).
b) Vì \(BE//AD\) nên \(\frac{{BD}}{{DC}} = \frac{{AE}}{{AC}}\).
Mà tam giác \(BAE\) cân tại \(A\) nên \(AE = AB \Rightarrow \frac{{AE}}{{AC}} = \frac{{AB}}{{AC}}\) (định lí Thales)
Do đó, \(\frac{{DB}}{{DC}} = \frac{{AE}}{{AC}} = \frac{{AB}}{{AC}}\) (điều phải chứng minh).