
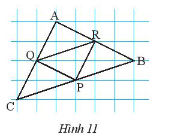
Cho biết cạnh mỗi ô vuông bằng \(1cm\). Tính độ dài các đoạn \(PQ,PR,RQ,AB,BC,CA\) trong Hình 11.

- Đường trung bình của tam giác là đoạn thẳng nối hai trung điểm của tam giác.
- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Định lí Py – ta – go cho tam giác vuông.

Đoạn thẳng \(AB\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{B^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AB = \sqrt {20} = 2\sqrt 5 \)
Đoạn thẳng \(AC\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{C^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AC = \sqrt {20} = 2\sqrt 5 \)
Đoạn thẳng \(BC\) là đường chéo của hình chữ nhật với chiều dài là \(6cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(B{C^2} = {2^2} + {6^2} = 4 + 36 = 40 \Rightarrow BC = \sqrt {40} = 2\sqrt {10} \)
Advertisements (Quảng cáo)
Từ hình vẽ ta thấy:
\(Q\) là trung điểm của \(AC\);
\(R\) là trung điểm của \(AB\);
\(P\) là trung điểm của \(BC\).
- Vì \(Q\) là trung điểm của \(AC\); \(R\) là trung điểm của \(AB\) nên \(QR\) là đường trung bình của tam giác \(ABC \Rightarrow QR = \frac{1}{2}BC\) (tính chất đường trung bình)
\( \Leftrightarrow QR = \frac{1}{2}.2\sqrt {10} = \sqrt {10} \left( {cm} \right)\).
- Vì \(Q\) là trung điểm của \(AC\); \(P\) là trung điểm của \(BC\) nên \(QP\) là đường trung bình của tam giác \(ABC \Rightarrow QP = \frac{1}{2}AB\) (tính chất đường trung bình)
\( \Leftrightarrow QP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)\).
- \(R\) là trung điểm của \(AB\); \(P\) là trung điểm của \(BC\) nên \(RP\) là đường trung bình của tam giác \(ABC \Rightarrow RP = \frac{1}{2}AC\) (tính chất đường trung bình)
\( \Leftrightarrow RP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)\).
