Cho \(\Delta ABC\), một đường thẳng song song với \(BC\) cắt \(AB\) và \(AC\) lần lượt tại \(D\) và \(E\). Qua \(E\) kẻ đường thẳng song song với \(CD\) cắt \(AB\) tại \(F\). Biết \(AB = 25cm,AF = 9cm,EF = 12cm\), độ dài đoạn \(DC\) là
A. 25cm.
B. 20cm.
C. 15cm.
D. 12cm.
- Định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
- Hệ quả của định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Chọn đáp án B
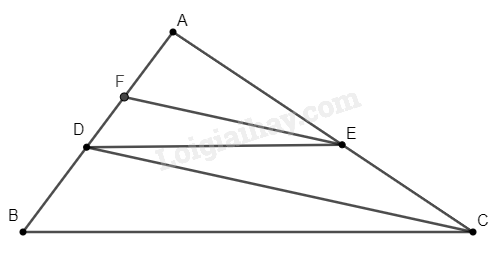
Xét tam giác \(ADC\) có \(EF//DC\), theo định lí Thales ta có:
\(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}}\) (1)
Xét tam giác \(ABC\) có \(DE//BC\), theo định lí Thales ta có:
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) (2)
Từ (1) và (2) suy ra,
\(\frac{{AF}}{{AD}} = \frac{{AD}}{{AB}} \Rightarrow AF.AB = A{D^2} \Leftrightarrow 9.25 = A{D^2} \Rightarrow AD = \sqrt {9.25} = 15\)
Xét tam giác \(ADC\) có \(EF//DC\), theo hệ quả định lí Thales ta có:
\(\frac{{AF}}{{AD}} = \frac{{EF}}{{DC}} \Rightarrow \frac{9}{{15}} = \frac{{12}}{{DC}} \Leftrightarrow DC = \frac{{12.15}}{9} = 20\)
Vậy \(DC = 20cm\).