Bài 34. Dựng tam giác ABC, biết .... Bài 34 trang 77 - Sách giáo khoa toán 8 tập 2 - Trường hợp đồng dạng thứ hai
Bài 34. Dựng tam giác ABC, biết \(\widehat{A}\) = 600 và, tỉ số đường cao \(\frac{AB}{AC}\) = \(\frac{4}{5}\) và đường cao AH = 6cm.

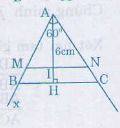
Trên hai cạnh Ax, Ay của góc \(\widehat{xAy}\) đặt AM = 4 đơn vị, AN = 5 đơn vị. Kẻ đường cao AH của ∆AMN.
Advertisements (Quảng cáo)
Trên tia AI lấy điểm H sao cho AH = 6cm, qua H vẽ đường song song với MN cắt Ax, Ay lần lượt tại B và C => ∆ABC thỏa mãn điều kiện để bài
Thật vậy:
MN // BC => ∆AMN ∽ ∆ABC => \(\frac{AM}{AN}\) = \(\frac{AB}{AC}\) = \(\frac{4}{5}\)
Vậy AH ⊥ BC, AH = 6cm => AH là đường cao.
