Advertisements (Quảng cáo)
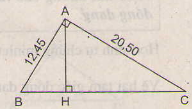
Bài 49 Ở hình 51, tam giác ABC vuông tại A có đường cao AH
a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng?.
b) Cho biết: AB = 12,45 cm, AC = 20,50cm. Tính độ dài các đoạn BC, AH, BH và CH.
a) ∆ABC ∽ ∆HBA vì \( \widehat{A}\) = \( \widehat{H}\) = 900 ,\( \widehat{B}\) chung
∆ABC ∽ ∆HAC vì \( \widehat{A}\) = \( \widehat{H}\) = 900, \( \widehat{C}\) chung
b) ∆ABC vuông tại A => BC2 = AB2 + AC2
=> BC2 = 12,452 + 20,502 = 575,2525
Advertisements (Quảng cáo)
=> BC= √575,2525 ≈ 24 cm
∆ABC ∽ ∆HBA
=> \( \frac{AB}{HB}\) = \( \frac{BC}{BA}\) => HB = \( \frac{AB^{2}}{BC}\) ≈ \( \frac{12,45^{2}}{24}\) ≈ 6,5 cm
=> CH = BC – BH = 24 – 6,5 ≈ 17,5 cm.
Mặt khác: \( \frac{AC}{AH}\) = \( \frac{AB.AC}{BC}\) = \( \frac{12,45.20,25}{24}\)
=> AH = 10,6 cm